Kleene* Operation#
Let us define the Kleene operation:
is another way for saying repeated concatenation. is the set of strings that are some concatenation of strings of :
The empty string is always in .
Example: Let .
In this case,
Theorem: The class of regular languages is closed under Kleene
Proof: Consider a regular language A, and let be a DFA accepting it. We will prove by constructing an NFA that accepts .
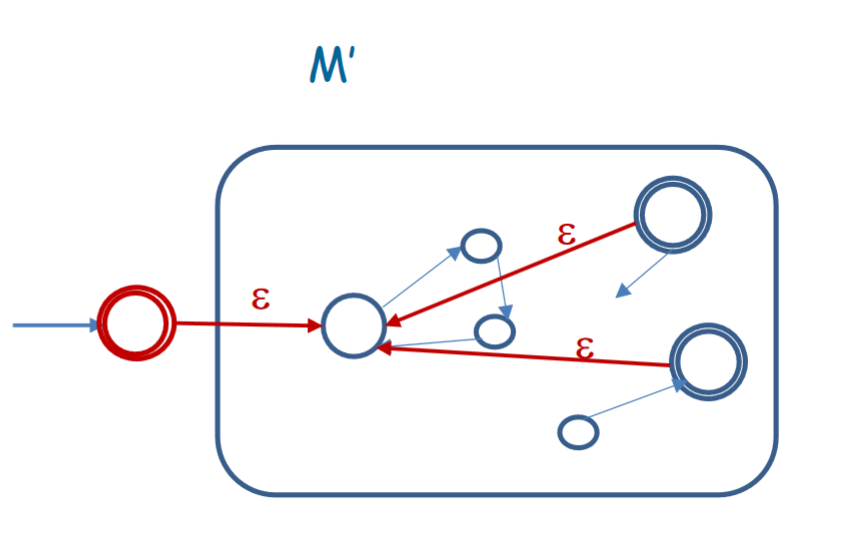
Given an input , needs to check if we can split into parts such that each part is accepted by . To do this, let us begin executing on . When the current state is an accepting state, we decide nondeterministically to switch to the initial state and restart on the rest of the string using an transition. If we end the string at an accepting state at some thread, that means that either the entire string was valid under , or it was split into parts that were valid under . The construction looks something like this:
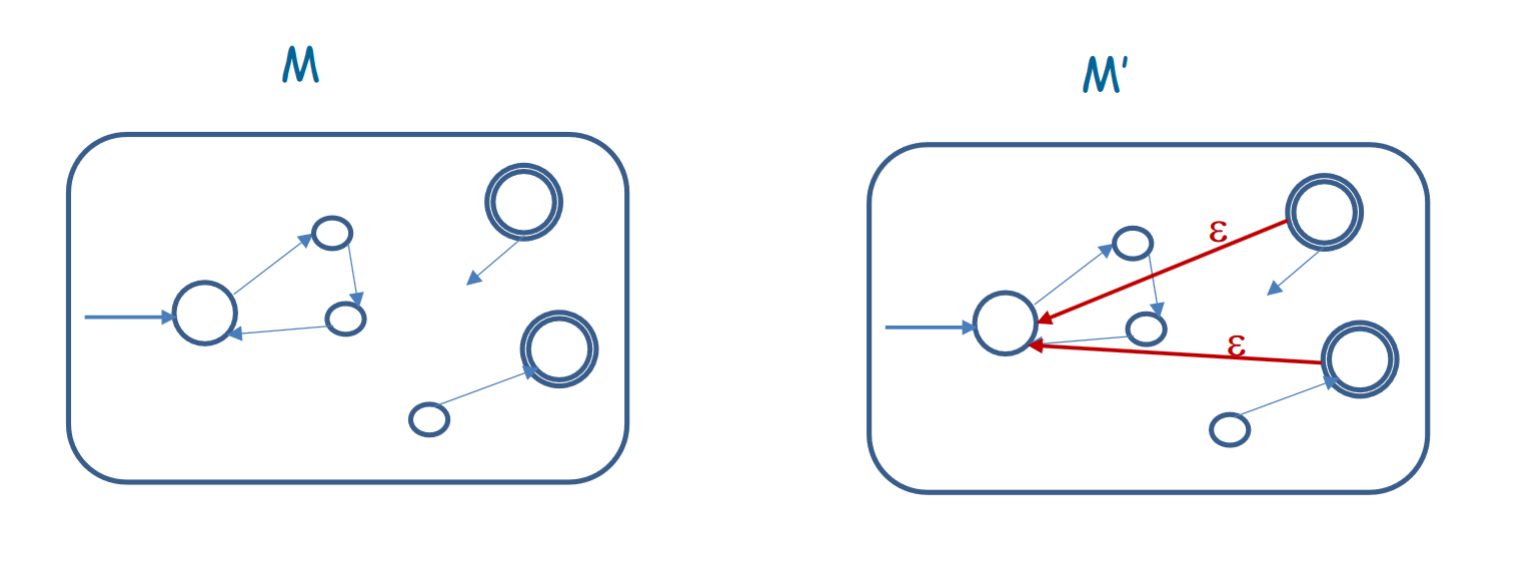
However, we have an issue. This construction might reject , which is always in . However, this is an easy solution. All we need to do is begin with an accepting state that has an transition to the initial state of . This way, if we have an empty string, it will automatically be valid, since it starts at an accepting state. However, if there are characters left in the string, it is forced to move forward, since there are no other threads for characters left at that state.